Introduction
Researchers and bodybuilders alike have long searched for the best ways to promote muscle growth. The last 20-years or so have involved a paradigm shift from the muscle damage hypothesis to the mechanical tension hypothesis. Essentially, we used to think that muscles grew following repair from damaging training, but now, we believe that the tension that causes muscle damage is the main stimulus for growth. Check out our What Causes Growth article here for a refresher on the entire topic – that particular article is a quick dissection of a much more in-depth review from Wackerhage et al. (2019).
Regardless, we’ve mostly centered on mechanical tension being the primary stimulus for growth. While that sounds great from a research standpoint, what is mechanical tension? How can we promote it? Is there any way to know we’re achieving enough? We’ll try to layout some theoretical groundwork in this piece that might get us down the path of answering some of these questions.
What is Mechanical Tension?
In short, mechanical tension is any force that tries to stretch our muscles – more often than not, this force is gravity unless we’re doing some sort of resistance training where the load itself is also trying to stretch our muscles (Beardsley, 2018). With this in mind, a muscle usually has to be performing some type of contraction to experience mechanical tension, whether that be eccentric, isometric, or concentric – muscles can also lengthen passively through things like static stretching and can change shape due to impacts, etc. We’re mostly sure that a muscle fiber has to be active for it to experience significant mechanical tension, so it’s important to outline mechanical tension by contraction type. When the same load is lifted in the three types of contractions, we typically see the highest activation during the concentric portion (Pasquet et al., 2006). This is due to the fact that we can produce more force isometrically and eccentrically and, therefore, don’t need as much activation during these portions of a lift to overcome the resistance. In addition, it requires less force production to lower or hold a weight as opposed to lifting it. Imagine that you’re benching 200lbs – you have to produce less than 200lbs of force to lower the bar, but more than 200lbs of force to press it.
 Why is mechanical tension [probably] the most important stimulus for growth? Well, think about the one constant force we have to resist throughout life: gravity. Our bodies have evolved with the constant stress of gravity and, thus, our muscle cells have developed mechanoreceptors that are tuned to detect changes in tension (Burkholder, 2007). If we constantly overload our muscles with tension (lift weights), these mechanoreceptors signal increased levels of stress which leads to long term adaptations (growth).
Why is mechanical tension [probably] the most important stimulus for growth? Well, think about the one constant force we have to resist throughout life: gravity. Our bodies have evolved with the constant stress of gravity and, thus, our muscle cells have developed mechanoreceptors that are tuned to detect changes in tension (Burkholder, 2007). If we constantly overload our muscles with tension (lift weights), these mechanoreceptors signal increased levels of stress which leads to long term adaptations (growth).
We can see the importance of mechanical tension really highlighted in bed rest studies. We know that bed rest (hospital situations, etc.) can cause massive amounts of muscle loss (Berg et al., 2007) due to gravity being almost completely taken out of the equation of daily life. We see similar results with astronauts returning from space (LeBlanc et al., 1995) and space programs have even developed resistance training programs for long-term space flight to combat this loss of constant tension (Hackney et al., 2015).
Mechanical tension also probably highly influences the other two proposed growth stimuli: metabolic stress and muscle damage. Muscle damage in isolation has been mostly phased out as a stimulus for growth at this point. However, an overload of mechanical tension will likely induce muscle damage so it’s tough to say whether or not the damage itself affects long-term growth (Wackerhage et al., 2019). In addition, metabolic stress is the burning sensation you feel during high rep lifting or even some forms of cardio. Metabolic stress typically increases muscle activation due to the acceleration of fatigue (Schoenfeld, 2013). Which, in turn, promotes greater mechanical tension due to more active muscle fibers!
All-in-all, mechanical tension is almost always referred to as the most important stimulus for muscle growth (Wackerhage et al., 2019). This is especially evident when comparing the training styles of a bodybuilder and marathon runner. The runner undergoes much, much more training volume, endures more metabolic stress, and probably deals with similar levels of muscle damage. However, the bodybuilder has larger muscles. Why? Resistance training involves high levels of mechanical tension!
Therefore, mechanical tension is of great interest to both bodybuilders and researchers alike. With this in mind, how might we quantify mechanical tension?
Why Quantify It?
First off, we need to discuss why we would quantify mechanical tension. Up to this point in this article, mechanical tension is just some abstract concept. We can’t attach a number to it and, therefore, can’t explain the muscle growth potential of a given exercise compared to another. Quantifying mechanical tension is also incredibly important for tracking load and fatigue throughout a training program.
Typically, we track training loads through reps x load lifted for all of our exercises. However, that doesn’t necessary reflect the mechanical challenge imposed by the training session as, again, a marathon runner would have a much higher training volume than a bodybuilder. It’s also not particularly useful for tracking progressive overload. We know that more volume doesn’t necessarily reflect more growth, especially if you’re just adding a bunch of wasted reps to your training program. With this in mind, some researchers have added barbell displacement to their training load calculations to try and better quantify training load (Hornsby et al., 2018). This could certainly help account for tracking both ROM and load, but it still doesn’t explain all factors of mechanical tension.
With these shortcomings in mind, let’s try to develop a theoretical framework for how we might quantify mechanical tension for a given exercise.
How Could we Quantify It?
For this theory, I think there’s four main factors we have to account for when attempting to quantify mechanical tension: muscle activation, biomechanical stress, range of motion, and contraction speed. Let’s get into each and how they might impact mechanical tension.
Muscle Activation
We know from earlier that muscle fibers [probably] have to be active in order to experience significant tension that triggers growth. We see solid support of this theory from a study by Wakahara et al. (2012) in which they found that the most active portion of a muscle grew the most from a long-term training program. However, activation is also massively influenced by biomechanical stress, which we’ll go over in the next section.
Regardless, the best support for muscle activation playing a role in mechanical tension is the old, “if you don’t use it, you lose it,” adage. We know muscle mass declines drastically in older age, and that sedentary adults lose muscle at a faster rate than active adults (Gianoudis et al., 2015). Again, this is gravity playing a role, but simply being active forces us to activate our muscles against the force of gravity and helps aging adults maintain their muscle mass.
So far, it’s looking like muscle activation plays an important role in quantifying mechanical tension. However, it’s certainly not the end-all, be-all. When we measure muscle activation, we typically use surface EMG electrodes, which are designed to detect electrical signals in the muscle. Unfortunately, there isn’t always a direct relationship between muscle activation and EMG data, especially in submaximal but fatiguing scenarios (Vigotsky et al., 2017). A better case for showing the potential of activation to play a large role is a classic study from Sundstrup et al. (2012) in which they found that muscle activation slowly increases over a set to failure and plateaus somewhere around 3-5 reps from failure. I think those last 3-5 reps are where activation and EMG data may not exactly line up, but it’s clear to see that effort can be represented by activation, at least in part.
All-in-all, I think muscle activation plays a crucial role in quantifying mechanical tension, but it’s not the lone component. Let’s get into biomechanical stress next.
Biomechanical Stress
Essentially, the biomechanical stress a muscle experiences in an exercise is dependent on the physics of the exercise (Chiu, 2018). For a quick brain pump, check out our Physics and Bodybuilding article here for a refresher. In short, physics can dictate the stress our muscle experiences in an exercise through “moments.” When we lift a weight, the weight exerts a force on our joints that is equivalent to the weight multiplied by its horizontal distance from the joint in question. This an “external moment.” On the flip side, our muscle produces force, which we then multiply by the distance between the muscle attachment and joint in question to uncover the “internal moment.”
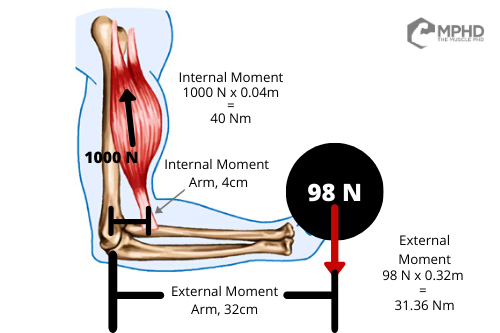 Why is this important? Well, we know that a muscle [probably] has to be active to experience tension and we know that the more force a muscle produces, the more tension it experiences – hence why bodybuilders grow, and runners do not. Therefore, it’s easy to see how moments can direct force production by a muscle; the greater the external moment, the larger the internal moment that’s required to lift the object. How do we create a larger internal moment? Well, unless you have great connections to a shady surgeon, the only way you can create a larger internal moment is by producing more muscular force.
Why is this important? Well, we know that a muscle [probably] has to be active to experience tension and we know that the more force a muscle produces, the more tension it experiences – hence why bodybuilders grow, and runners do not. Therefore, it’s easy to see how moments can direct force production by a muscle; the greater the external moment, the larger the internal moment that’s required to lift the object. How do we create a larger internal moment? Well, unless you have great connections to a shady surgeon, the only way you can create a larger internal moment is by producing more muscular force.
How does this play out in the real world? We see studies showing that front squats cause just as much quad activation as back squats, even when using less weight (Gullett et al., 2009). Why is this the case? Front squats impose a greater external moment at the knee; therefore, more quad activation is required to overcome the resistance (Gullett et al., 2009). Similarly, moving from a wide grip to narrow grip bench grip increases triceps activation (Barnett et al., 1995; Lehman, 2005) without any change to the weight being lifted. This is also why we see greater upper pec activation in close grip and incline bench variations (Barnett et al. 1995) – these variations impose a greater shoulder flexion requirement that is entirely influenced by biomechanics, rather than weight.
Realistically, the biomechanics of an exercise are probably more important than muscle activation since mechanics directly influence activation. However, we have a lot more published data on muscle activation than biomechanics when it comes to lifting. Frankly, muscle activation is much easier to measure and researchers can pump those studies out in no time. Biomechanics studies take a much longer time and involve clicking dots on screens for hours on end.
There’s one major area where biomechanics and activation can’t explain everything, though. Research shows us that the glutes experience their greatest internal moment at near full hip extension (Nemeth, 1984) which is why we see glute activation being high in exercises like hip thrusts (Contreras et al., 2015) and higher in quarter squats compared to deep squats (da Silva et al., 2017). However, studies have shown that we get greater glute growth from deep squats than quarter squats (Bloomquist et al., 2013; Kubo et al., 2019) and we even have one study showing greater glute growth from deep squats than hip thrusts (Barbalho et al., 2020) – unfortunately, that particular study has some murky questions surrounding its results (Vigotsky et al., 2020). Check our Hip Thrusts vs. Squats article here for more info on that.
With this shortcoming in mind, it’s time to talk about range of motion.
Range of Motion
Range of motion is a pretty similar discussion to biomechanics as the ROM of an exercise can largely influence its biomechanics. For instance, a deep squat imposes a greater range of motion at the knee joint than a shallow squat which results in a greater mechanical challenge at the knee (Bryanton et al., 2012). Studies show that deep squats induce more quad growth than shallow squats (Bloomquist et al., 2013; Kubo et al., 2019) even when using matched loads (based on relative percentages). This could also be why we see greater glute growth in deep squats than shallow squats, and possibly squats over hip thrusts (but we’ll have to wait for more data on that). Is range of motion more important than biomechanics when concerning mechanical tension?
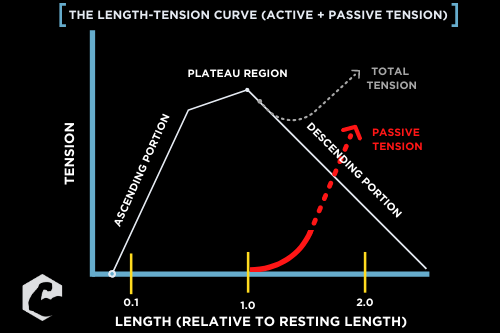 In short, we can’t really rank them since they pretty much end up being one and the same. Taking an exercise through a larger range of motion will almost always impose a greater biomechanical stress on a given muscle group. The larger range of motion will also force muscle fiber deformation longitudinally which can influence how our muscles grow (Franchi et al., 2017). In addition, a larger range of motion will increase passive loading through the length-tension curve (on the right). This is important as each muscle group in our body can only actively produce force on a certain segment of this curve. Anything beyond a muscle’s maximum active length is considered “passive tension” and is mostly detected by the third contractile protein, titin (van der Pijil et al., 2018). This is one caveat where muscle fibers might not have to be technically active to grow, but that’s probably worth an entire article on its own.
In short, we can’t really rank them since they pretty much end up being one and the same. Taking an exercise through a larger range of motion will almost always impose a greater biomechanical stress on a given muscle group. The larger range of motion will also force muscle fiber deformation longitudinally which can influence how our muscles grow (Franchi et al., 2017). In addition, a larger range of motion will increase passive loading through the length-tension curve (on the right). This is important as each muscle group in our body can only actively produce force on a certain segment of this curve. Anything beyond a muscle’s maximum active length is considered “passive tension” and is mostly detected by the third contractile protein, titin (van der Pijil et al., 2018). This is one caveat where muscle fibers might not have to be technically active to grow, but that’s probably worth an entire article on its own.
All-in-all, coaches are already including range of motion in load calculations (Hornsby et al., 2018) as the range of motion of an exercise can largely influence muscle damage and recovery needs (Baroni et al., 2017). While that’s important for fatigue management, ROM also plays a role in mechanical tension through its interaction with the biomechanics of an exercise and also largely determines how much time a muscle spends under a given amount of tension.
Contraction Speed
The last main component that probably influences mechanical tension is the contraction speed of an exercise. Why does this matter? We need to consider the force velocity curve. This curve tells us how much force a muscle can produce at a given velocity. It’s easy to see that a muscle produces its highest level of concentric force at slower contraction speeds. Why is this the case?
When a muscle contracts slowly, it has plenty of time to create actin-myosin cross bridges. The more interaction between actin and myosin that you can get, the more force your muscle will produce!
The easiest way to see the difference between contraction speeds is comparing jumping vs. heavy lifting. Both practices actually involve high levels of muscle activation but jumping doesn’t lead to muscle growth (Eftestol et al., 2016). This is another example of activation not necessarily reflecting tension, but it also underlines the importance of contraction speed in regard to growth. Fibers have to be active and contracting slowly to experience large levels of tension.
Now, people often take this the wrong way and assume they need to purposefully move slow in order to increase force production in an exercise. Unfortunately, purposefully moving slow will also reduce muscle activation. Increasing the number of inactive fibers in an exercise will simply reduce the growth stimulus of that exercise and will likely only activate slow twitch fibers which don’t grow as easily as fast twitch fibers (Van Wessel et al., 2010). With this in mind, the contraction speed of an exercise needs to either be dictated by load or fatigue. We know that heavy loads will force slower contraction speeds, and we also know that fatigue will force slower contractions as well (Sanchez-Medina et al., 2011). And, just for kicks and giggles, we know that loads of 80% 1RM and up maximize muscle activation in a similar manner to lighter loads taken to within 3-5 reps to failure (Sundstrup et al., 2012). Funny how everything eventually lines up, isn’t it?
“Practical” Applications
Here’s when everything we’ve talked about gets, ahem, a little murky. How practical is all of this? Is it really worth the time to create a 4-part equation for quantifying mechanical tension? Do normal people even have the equipment necessary to perform these calculations? In short, probably not. But there’s plenty of impractical science in our field so let’s soldier on and discuss how we might use all of the above to quantify mechanical tension.
- First, we’d probably want the activation percentage of each rep in a given exercise. This would probably have to be expressed as a % of a maximum voluntary isometric contraction (MVIC) to help make it more relative to other movements. Unless you have EMG electrodes on hand, you probably can’t do this. Regardless, for this example, let’s assume you performed leg extensions for a heavy set of 8 reps with an average activation % of 85%.
- Second, we need to know the external moment of the exercise so we can calculate how much force the muscle is having to overcome. This portion is important as it accounts for both the weight and the mechanical difficulty of the exercise. Again, unless you have a 3-D camera system and reflective markers, good luck even getting a start on this calculation. Plus, you’d have to take the average moment of every video frame which would probably take about an hour to track on slow motion video. Regardless, let’s give a very arbitrary number here and say our average external moment was 250 Nm on each rep.
- Third, we need to track the range of motion for the joint in question. This is a gray area where it’s tough to say whether we use degrees of rotation at the given joint, or if we would simplify to something like load displacement. However, I think degrees of rotation at a specific joint is probably going to be more accurate for the muscle group in question, especially for compound exercises where form might get sloppy close to failure. This would lead us see that mechanical tension can actually drop in the last few reps to failure since joint ROM might be reduced. Therefore, you’d again need some sort of 3-D camera system to track the sum of rotation at the joint – the knee in this leg extension example. Let’s assume you underwent an average of 120-degrees of rotation in each rep (90 to 150 back to 90).
- Lastly, we need the contraction speed. To perfectly assess muscle contraction speed, we’d need technology that virtually no one has, so we’d probably default to something like a Tendo unit that can track barbell velocity. We could technically track rotational speed at the joint as well, but a Tendo is, like, the one easily applicable thing we have in this equation. In the leg extension, we’d simply attach the Tendo unit to the ankle pad and would track the average velocity in meters per second. However, since our goal is slow contraction speeds, we’d probably want to divide the product of the first three numbers by whatever speed we get in this section. For this example, let’s assume your average velocity over your 8 reps of leg extensions was 0.55m/s.
All-in-all, this equation would probably have to look something like:
Activation Percentage x (External Moment x Joint ROM) / Contraction Velocity
So, in our example:
0.85 x (250N x 120deg) / 0.55m/s = 46,363.63 mechanical tension units
Since that’s a massive number, let’s just do the ol’ kilocalories labeled as calories trick and break that down to 46.36 [kilo] mechanical tension units. Until we have an order of importance on each factor involved, everything needs to be multiplied or divided, rather than added or subtracted. This ensures that changing any of the factors will affect the final outcome in a relative fashion.
This could also be where one could push for having the range of motion of the movement measured by distance (in m), rather than degrees of rotation – OR, one could push for measuring contraction velocity by joint rotation speed (deg/s). Either one would simplify the end unit to N/s which certainly sounds fancy. Fancy isn’t necessarily better, though.
And, no, this isn’t practical at all, hence the quotations marks in the section title. This is simply the scientific method at work – create a theory that’s nearly impossible to actually use, and we’ll slowly whittle our way down to something that can actually help people.
More “Stuff” to Consider
 Since we’ve already complicated this process this much, we might as well add a few more impossibly high hurdles when covering mechanical tension.
Since we’ve already complicated this process this much, we might as well add a few more impossibly high hurdles when covering mechanical tension.
First, we would also technically have to consider antagonist activation in an equation for mechanical tension. Muscles don’t just overcome external forces (weight), but they also have to overcome the force of the co-contraction of an opposing muscle. For instance, when you do a leg extension, you’re going to get a small amount of hamstrings activation to help stabilize and protect the knee joint (Aagaard et al., 2000). Technically, this co-activation would add to the total external moment a muscle has to overcome and, thus, would influence mechanical tension. However, I think we can probably leave this out of the equation for now unless we want to throw in EMG of the opposing muscle group somehow. This could reflect an increase in mechanical tension as one accrues training experience since antagonist activation is typically reduced over time (Behm et al., 2002). Alas, this would also be mostly pointless to track overtime when considering progressive overload.
We also have to always keep in mind that mechanical tension is detected by individual muscle fibers, rather than the whole muscle (Burkholder, 2007). Remember, growth happens at the individual fiber level, not the whole muscle itself (Trappe et al., 2000). Therefore, since contraction of a whole muscle causes the muscle to bulge, each individual fiber is going to be affected by the fibers bulging around it. Since fiber bulging could also influence mechanical tension (by deforming neighbor fibers), technically we’d have to also consider this in our equation. However, this is even more implausible than what we’ve already presented, so I don’t think it’s a big deal – just need to satisfy the occasional super nerd reader.
Conclusion
Mechanical tension is incredibly important for muscle growth, but we have no way of quantifying this important factor. How can we know when we’ve truly overloaded a muscle? You’d need some sort of equation involving the four items we discussed in this piece: muscle activation, the external moment of the exercise, the ROM of the exercise, and the contraction speed. For now, each component is equally important to the mechanical tension equation, so changing any of these factors can greatly affect the overall outcome.
If you’ve made it to the end of this piece, great job! This is another piece that we’ll probably keep updating and working on as go. Eventually, we’d love to publish a legitimate review of the topic but starting at a more lay level is often helpful for developing a more applicable theory.
The main takeaway from this piece, then, is to simply focus on increasing the four components of mechanical tension as much as possible in your training. Train with heavy loads or close to failure to maximize muscle activation. Use exercises that have large external moment arms to train certain muscle groups (high bar squats vs. low bar squats for the quads, for example). Use larger ranges of motion to increase mechanical difficulty and maximize longitudinal hypertrophy. And, lastly, make sure you’re using slow contraction velocities that are either dictated by load or fatigue. Really, all of these components are pretty easy to sum up by simply saying, “Train hard and use good form.”
Easter Egg
We typically just use a numbering system for our in-text citations but since we’re anticipating a ton of updates to this article over the next few years, it was easier to leave in normal APA in-text format. We apologize for the wordier appearance, but it keeps things easier to work with on our end!
References
- Aagaard, P., Simonsen, E. B., Andersen, J. L., Magnusson, S. P., Bojsen‐Møller, F., & Dyhre‐Poulsen, P. (2000). Antagonist muscle coactivation during isokinetic knee extension. Scandinavian Journal of Medicine & Science in Sports, 10(2), 58-67.
- Barbalho, M., Coswig, V., Souza, D., Serrao, J. C., Campos, M. H., & Gentil, P. (2020). Back squat vs. hip thrust resistance-training programs in well-trained women. International Journal of Sports Medicine, 41(05), 306-310.
- Barnett, C., Kippers, V., & Turner, P. (1995). Effects of variations of the bench press exercise on the EMG activity of five shoulder muscles. The Journal of Strength & Conditioning Research, 9(4), 222-227.
- Baroni, B. M., Pompermayer, M. G., Cini, A., Peruzzolo, A. S., Radaelli, R., Brusco, C. M., & Pinto, R. S. (2017). Full range of motion induces greater muscle damage than partial range of motion in elbow flexion exercise with free weights. The Journal of Strength & Conditioning Research, 31(8), 2223-2230.
- Beardsley, C. (2018). What determines mechanical tension during strength training? https://medium.com/@SandCResearch/what-determines-mechanical-tension-during-strength-training-acdf31b93e18
- Behm, D. G., Anderson, K., & Curnew, R. S. (2002). Muscle force and activation under stable and unstable conditions. The Journal of Strength & Conditioning Research, 16(3), 416-422.
- Berg, H. E., Eiken, O., Miklavcic, L., & Mekjavic, I. B. (2007). Hip, thigh and calf muscle atrophy and bone loss after 5-week bedrest inactivity. European Journal of Applied Physiology, 99(3), 283-289.
- Bloomquist, K., Langberg, H., Karlsen, S., Madsgaard, S., Boesen, M., & Raastad, T. (2013). Effect of range of motion in heavy load squatting on muscle and tendon adaptations. European Journal of Applied Physiology, 113(8), 2133-2142.
- Bryanton, M. A., Kennedy, M. D., Carey, J. P., & Chiu, L. Z. (2012). Effect of squat depth and barbell load on relative muscular effort in squatting. The Journal of Strength & Conditioning Research, 26(10), 2820-2828.
- Burkholder, T. J. (2007). Mechanotransduction in skeletal muscle. Frontiers in Bioscience: A Journal and Virtual Library, 12, 174.
- Chiu, L. Z. (2018). Biomechanical methods to quantify muscle effort during resistance exercise. The Journal of Strength & Conditioning Research, 32(2), 502-513.
- Contreras, B., Vigotsky, A. D., Schoenfeld, B. J., Beardsley, C., & Cronin, J. (2015). A comparison of gluteus maximus, biceps femoris, and vastus lateralis electromyographic activity in the back squat and barbell hip thrust exercises. Journal of Applied Biomechanics, 31(6), 452-458.
- da Silva, J. J., Schoenfeld, B. J., Marchetti, P. N., Pecoraro, S. L., Greve, J. M., & Marchetti, P. H. (2017). Muscle activation differs between partial and full back squat exercise with external load equated. The Journal of Strength & Conditioning Research, 31(6), 1688-1693.
- Eftestøl, E., Egner, I. M., Lunde, I. G., Ellefsen, S., Andersen, T., Sjåland, C., … & Bruusgaard, J. C. (2016). Increased hypertrophic response with increased mechanical load in skeletal muscles receiving identical activity patterns. American Journal of Physiology-Cell Physiology, 311(4), C616-C629.
- Franchi, M. V., Reeves, N. D., & Narici, M. V. (2017). Skeletal muscle remodeling in response to eccentric vs. concentric loading: morphological, molecular, and metabolic adaptations. Frontiers in Physiology, 8, 447.
- Gianoudis, J., Bailey, C. A., & Daly, R. M. (2015). Associations between sedentary behaviour and body composition, muscle function and sarcopenia in community-dwelling older adults. Osteoporosis International, 26(2), 571-579.
- Gullett, J. C., Tillman, M. D., Gutierrez, G. M., & Chow, J. W. (2009). A biomechanical comparison of back and front squats in healthy trained individuals. The Journal of Strength & Conditioning Research, 23(1), 284-292.
- Hackney, K. J., Scott, J. M., Hanson, A. M., English, K. L., Downs, M. E., & Ploutz-Snyder, L. L. (2015). The astronaut-athlete: optimizing human performance in space. The Journal of Strength & Conditioning Research, 29(12), 3531-3545.
- Hornsby, W. G., Gentles, J. A., Comfort, P., Suchomel, T. J., Mizuguchi, S., & Stone, M. H. (2018). Resistance training volume load with and without exercise displacement. Sports, 6(4), 137.
- Kubo, K., Ikebukuro, T., & Yata, H. (2019). Effects of squat training with different depths on lower limb muscle volumes. European Journal of Applied Physiology, 119(9), 1933-1942.
- LeBlanc, A., Rowe, R., Schneider, V., Evans, H., & Hedrick, T. (1995). Regional muscle loss after short duration spaceflight. Aviation, Space, and Environmental Medicine, 66(12), 1151-1154.
- Lehman, G. J. (2005). The influence of grip width and forearm pronation/supination on upper-body myoelectric activity during the flat bench press. The Journal of Strength & Conditioning Research, 19(3), 587-591.
- Németh, G. (1984). On hip and lumbar biomechanics. A study of joint load and muscular activity. Scandinavian Journal of Rehabilitation Medicine. Supplement, 10, 1.
- Pasquet, B., Carpentier, A., & Duchateau, J. (2006). Specific modulation of motor unit discharge for a similar change in fascicle length during shortening and lengthening contractions in humans. The Journal of Physiology, 577(2), 753-765.
- Sanchez-Medina, L., & González-Badillo, J. J. (2011). Velocity loss as an indicator of neuromuscular fatigue during resistance training. Medicine & Science in Sports & Exercise, 43(9), 1725-1734.
- Schoenfeld, B. J. (2013). Potential mechanisms for a role of metabolic stress in hypertrophic adaptations to resistance training. Sports Medicine, 43(3), 179-194.
- Sundstrup, E., Jakobsen, M. D., Andersen, C. H., Zebis, M. K., Mortensen, O. S., & Andersen, L. L. (2012). Muscle activation strategies during strength training with heavy loading vs. repetitions to failure. The Journal of Strength & Conditioning Research, 26(7), 1897-1903.
- Trappe, S., Costill, D., & Thomas, R. (2000). Effect of swim taper on whole muscle and single muscle fiber contractile properties. Medicine and Science in Sports and Exercise, 32(12), 48-56.
- van der Pijl, R., Strom, J., Conijn, S., Lindqvist, J., Labeit, S., Granzier, H., & Ottenheijm, C. (2018). Titin‐based mechanosensing modulates muscle hypertrophy. Journal of Cachexia, Sarcopenia and Muscle, 9(5), 947-961.
- Van Wessel, T., De Haan, A., Van der Laarse, W. J., & Jaspers, R. T. (2010). The muscle fiber type–fiber size paradox: hypertrophy or oxidative metabolism? European Journal of Applied Physiology, 110(4), 665-694.
- Vigotsky, A. D., Beardsley, C., Contreras, B., Steele, J., Ogborn, D., & Phillips, S. M. (2017). Greater electromyographic responses do not imply greater motor unit recruitment and ‘hypertrophic potential’ cannot be inferred. The Journal of Strength & Conditioning Research, 31(1), e1-e4.
- Vigotsky, A., Nuckols, G. L., Heathers, J., Krieger, J., Schoenfeld, B. J., & Steele, J. (2020). Improbable data patterns in the work of Barbalho et al. [White Paper]. https://osf.io/sg3wm/download
- Wackerhage, H., Schoenfeld, B. J., Hamilton, D. L., Lehti, M., & Hulmi, J. J. (2019). Stimuli and sensors that initiate skeletal muscle hypertrophy following resistance exercise. Journal of Applied Physiology, 126(1), 30-43.
- Wakahara, T., Miyamoto, N., Sugisaki, N., Murata, K., Kanehisa, H., Kawakami, Y., … & Yanai, T. (2012). Association between regional differences in muscle activation in one session of resistance exercise and in muscle hypertrophy after resistance training. European Journal of Applied Physiology, 112(4), 1569-1576.
From being a mediocre athlete, to professional powerlifter and strength coach, and now to researcher and writer, Charlie combines education and experience in the effort to help Bridge the Gap Between Science and Application. Charlie performs double duty by being the Content Manager for The Muscle PhD as well as the Director of Human Performance at the Applied Science and Performance Institute in Tampa, FL. To appease the nerds, Charlie is a PhD candidate in Human Performance with a master’s degree in Kinesiology and a bachelor’s degree in Exercise Science. For more alphabet soup, Charlie is also a Certified Strength and Conditioning Specialist (CSCS), an ACSM-certified Exercise Physiologist (ACSM-EP), and a USA Weightlifting-certified performance coach (USAW).




